VRP论文--"A Penalty Based Edge Assembly Memetic Algorithm for the Vehicle Routing Problem With Time Windows"

论文信息

Title: A penalty-based edge assembly memetic algorithm for the vehicle routing problem with time windows

Authors: $Yuichi\ Nagata^{a,*}, Olli\ Bräysy^b, Wout\ Dullaert^{c,d}$

Publication date: Available online 3 July 2009.

DOI: https://doi.org/10.1016/j.cor.2009.06.022

概要

介绍了一个针对VRPTW的模因算法(memetic algorithm)。主要思路是基于已有的EAX算子进行调整，并引入一种惩罚函数来消除由EAX算子产生后代中违反time window和capacity约束的情形。

虽然论文介绍的算法整体效率偏低，但依然有借鉴之出。

1. 介绍

论文发布时(2009.7.3)SOTA的精确算法: ¹, ², ³ , ⁴;精确算法在小规模下效果不错，在大规模实例下只能解决包含特定结构或者tw约束非常紧的实例。

论文发布时(2009.7.3)SOTA的启发式算法：进化策略 ⁵‘⁶, 大规模领域搜索 ⁷’⁸‘⁹, 迭代式局部搜索 ¹⁰’¹¹, 从多点出发的局部搜索 ¹⁰‘¹²；对于分层的目标通常使用 two-stage 方法¹³,⁷

two-stage approach: 通常第一个阶段对路线数量最小化，第二阶段对总行驶距离进行最小化。two-stage最大的好处是可以让我们独立的开发针对减车和减距离不同的算法。

模因算法(MA:memethic algorithm)¹⁴: 是一种基于种群的并联合演化算法(EA)可以在全局上探索更远，在局部搜索上更加密集。MAs通常被称为混合遗传算法或是遗传局部搜索

EAX: the edge assembly crossover，最早用于TSP¹⁵‘¹⁶’¹⁷,然后对CVRP进行适配¹⁸

EAMA: the edge assembly memetic algorithm for the CVRP¹⁸. 它也是two-stage。其初始种群个体路线数相同，由一个减车过程产生¹⁹，后续有一个减距离的过程。

1.1 临时的无效解以及惩罚函数

这篇论文是在EAMA的基础上将EAX算子增加了对tw约束的适配。在MAs过程中生成同时满足capacity和tw的可行后代解通常是很困难的。因此允许临时产生一个无效解是有意义的。通常我们引入一个惩罚函数来引导搜索向有效解靠拢。在启发式搜索中这是一个常见的概念。

1.2 可以在O(1)内计算的惩罚函数

在传统的领域算子下，计算路线的tw惩罚需要O(n)，n为路线中customer数量。这篇论文开发了一个在 O(1) 时间内计算tw惩罚函数的方法并且对大多数领域算子都有效。

2. 问题定义和记号

$G=(V,E)$: VRPTW定义了一个完全有向图
$V=\lbrace0,1,\ldots,N\rbrace$ : 顶点
$E=\lbrace (v,w)|v,w \in V(v\ne w)\rbrace$: 边
node 0表示 depot， nodes $\lbrace 1,\ldots,N \rbrace$表示customers
$q_v (v \in V)$: demand，$q_0 = 0$
$s_v$: service time, $s_0=0$
$[e_v,l_v]$ : time window
$(v,w)$ : edge
$d_{vw}$: 两点间行驶距离
$c_{vw}$: 两点间行驶时间
$Q$: the capacity of vehcile
给定一条路线$\langle v_0,v_1,\ldots,v_n,v_{n+1} \rangle$
- 路线满足 capacity 约束: $\sum_{i=1}^n q_{v_i} \le Q$
- $a_{v_i}$: depart time of $v_i$, defined as follow:

$$ a_{v_i} = \begin{cases} \ e_{v_0}, &i=0\\\
\max\lbrace a_{v_{i-1}} +s_{v_{i-1}}+c_{{v_{i-1}}{v_i}},e_{v_i}\rbrace, &i=1,\ldots,n+1 \end{cases} \tag{1}\label{1} $$

路线满足 tw 约束:$a_{v_i}\le l_{v_i}(i=0,…,n+1)$
$t(r)=\sum_{i=0}^n d_{v_i v_{i+1}}$ : 单条路线行驶距离
$\sigma$: 可行解,defined as follow:
- m: 条可行路线
- 每个customer 有且仅有一条路线访问
- $F(\sigma)=\sum_{r=1}^mt(r)$: 解的总行驶距离
$e_v+s_v+c_{vw} \ge l_w$ : 不可行边

3. 求解方法

这篇论文提到的EAMA由 EAMA for CVRP ²⁰扩展而来。最主要的特征是：

先用EAX算子产生可能违反约束的临时后代解；
再进行一个基于localsearch的repair过程使得临时的不可行解在广义的cost function(包含总距离和惩罚函数)下有所改进；
然后遵循标准的MA过程进行a simple localsearch 尝试改进得到的可行解。

3.1 EAMA概述

EAMA主要过程 Fig.1

m: 用车数，注意，所有父代的用车数都为m

RM¹⁹: route minimization heuristic for VRPTW.

子代替换策略: 从$N_{ch}$中的best替换 $p_A$。这种替换策略为了保持种群中的多样性，所以best并不替换种群中最差的个体。

随机性体现在: (1) 对父代随机排序 (2) EAX (2) Repair (2) Improve
这种随机比较盲目

EAX的成熟度与终止策略: EAX使用两种策略 single 和 block。先使用 single 策略，如果种群中的best在连续$g_{max}$代后未改进，则更换成block策略，同样连续$g_{max}$代无改进则终止迭代(R)。

3.2 广义cost函数

$$F_g(\sigma)=F(\sigma)+\alpha\cdot P_c(\sigma)+\beta\cdot P_{tw}(\sigma) \tag{2}$$ $F(\sigma)$: 总行驶距离

$P_c(\sigma)$: capacity惩罚项, 在传统的领域算子(如$\text{2-opt}^*$,Or-Exchange,Relocation,Exchange²¹)下计算时间为 O(1)，为解中超出capacity的总和, 定义如下: $$ P_c(\sigma)=\sum_{r=1}^m\lbrace\sum_{v\in {c u s t}(r)}q_v-Q,0\rbrace\tag{3} $$

$P_{tw}(\sigma)$: tw惩罚项

标准的TW惩罚项和新的TW惩罚项比较:

a. 标准的tw惩罚项计算, b. O(1)的tw惩罚项计算，方括号表示tw, 圆点表示$a_v$和$\tilde a_v$，箭头表示tw惩罚(delay)。 Fig.2 Fig 2

标准的路线tw惩罚项定义: $\sum_{i=0}^{n+1} \max \lbrace a_{v_i} - l_{v_i}\rbrace$, $a_{v_i}$定义见$\eqref{1}$，当发生neighborhood move时, 计算时间为 O(n).

新的tw惩罚项描述如下

$\tilde a_{v_i}$: extended depart time，定义如下:($a_{v_i}^\prime$: extended arrival time) $$ \begin{array} \tilde a_{v_i}^\prime = \begin{cases} \ e_0, &i=0\\\
\tilde a_{v_{i-1}} +s_{v_{i-1}}+c_{v_{i-1} v_i} & i=1,\ldots,n+1 \end{cases}\\\
\tilde a_{v_i} = \begin{cases} \max\lbrace \tilde a_{v_i}^\prime,e_{v_i}\rbrace, &if\ \tilde a_{v_i}^\prime\le l_{v_i} \\\
\tilde l_{v_i} &if\ \tilde a_{v_i}^\prime\gt l_{v_i} \end{cases} \end{array}\tag{4}\label{4} $$ 路线的tw惩罚： $$ TW(r)=\sum_{i=0}^{n+1}\max\lbrace \tilde a_{v_i}^\prime - l_{v_i},0\rbrace\tag{5}\label{5} $$ 解的tw惩罚项：$P_{t w}(\sigma)=\sum_{r=1}^m TW(r)$

1. 当路线是可行的时候,depart time在两种计算方式下相等, $\tilde a_{v_i} = a_{v_i}$
2. 如果某个node出现$\tilde a_{v_i}^\prime\gt l_{v_i}$,tw约束被违反了，也就是产生了一个delay。
3. 我们假设在记录惩罚$(\tilde a_{v_i}^\prime - l_{V_i})$的同时消除这个惩罚(delay)，即 depart time 可以前移到end time $l_{v_i}$
4. 如Fig 2中的一段path: $\langle v2,v3,v4\rangle$ 如果v2没有发生delay，那么v3,v4也不会发生delay，在新的计算方式中，v3,v4上的惩罚并不会记录。

新的TW惩罚项优势:

对于传统的neighborhood move,$P_{t w}(\sigma)$ 能在O(1)时间内计算,证明见命题1
能够恰当的评估一个优良的局部路径的TW约束。

3.3 EAX

EAX允许产生一个违反约束的子代。主要分为5个步骤，如下:

Fig.3

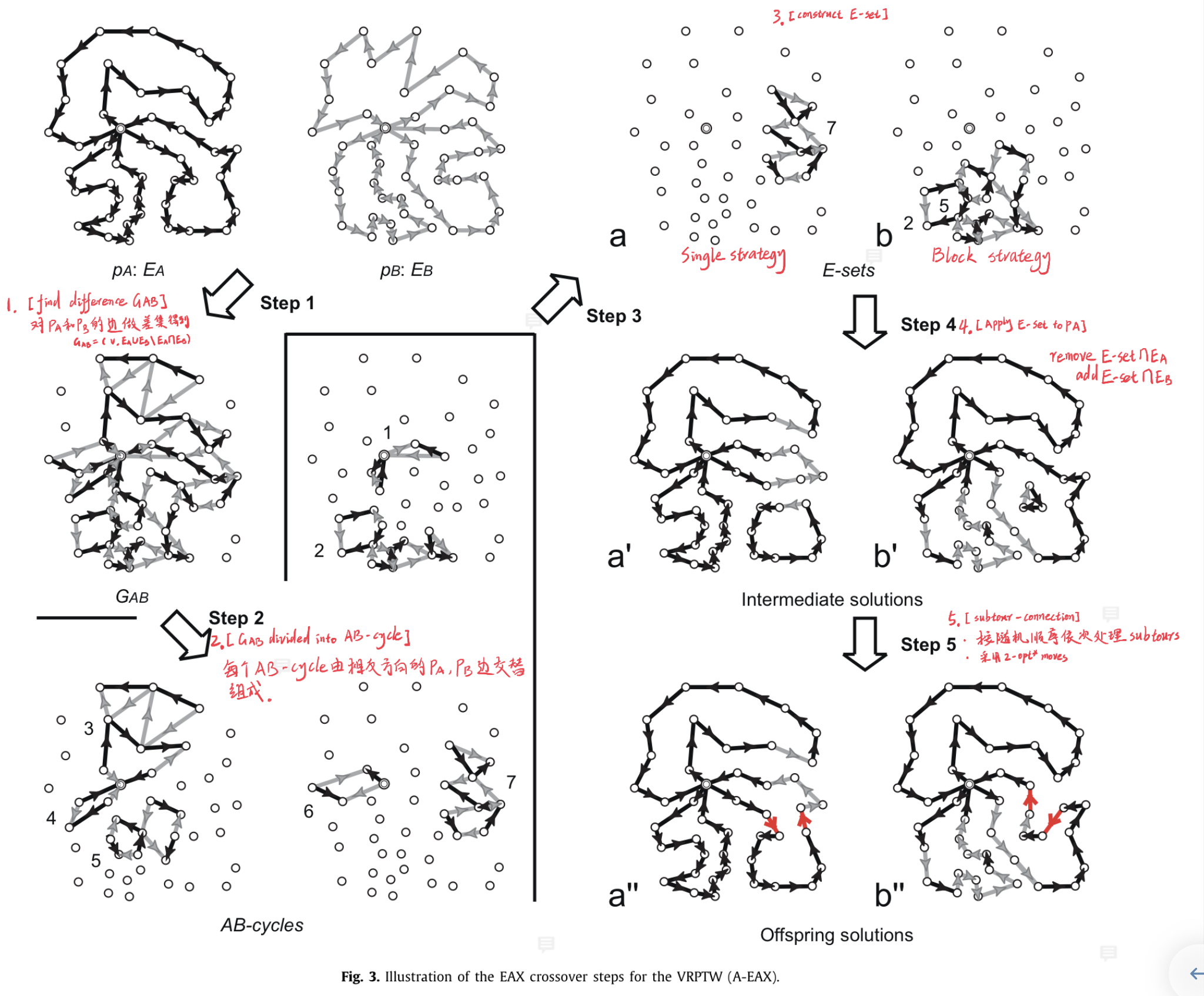
Step 1. [find difference graph $G_{A B}$]

$G_{A B}=(V,E_A\cup E_B\setminus E_A\cap E_B)$

Step 2. [generate AB-cycles]

AB-cycle 的形成过程:

从$G_{A B}$ 中随机选取一点为起点，依次按顺$p_A$方向，逆$p_B$方向选边，直到AB-cycle形成。
当node是custoemr时，可选的边是唯一确定的，当node是depot时,则随机选取一条边。
每次找到AB-cycle之后，相应的边从$G_{A B}$中移除。
持续这个过程直到$G_{A B}$中所有边都消失。

Step 3. [construct E-set]

Single 策略: 随机选择一个 single AB-cycle
Block 策略: 1. 随机选择一个single AB-cycle作为center AB-cycle. 2. 此外，再选择一个AB-cycle，要求至少和center AB-cycle共享一个customer node，并且node数少于center AB-cycle。

本质上，single 策略更适合相对局部的改进，而block 策略对全局的改进更有效。毕竟涉及的点更多。

Step 4. [Apply E-set to $p_A$]

remove E-set$\cap E_A$
add E-set$\cap E_B$

生成的临时解，含有m条从depot出发的路线和可能存在1个以上的subtours(不经过depot)

Step 5. [subtour-connect]

随机选取一个subtour，使用$\text{2-opt}^*$ moves²².（在subtour 和 tour中各选择一条边移除，且引入两条新的边，生成一条新路线，并保持方向一致。）
尝试所有的移除组合，并使得delta cost 最小
持续这个过程直到所有subtour都被连接

这里delta cost 只考虑距离
如果使得delta cost最小的move不是唯一，则重复step 3-5。？？？？

EAX for VRPTW 和 EAX for CVRP 的区别

和EAX for CVRP相比，最大的不同是 EAX for CVRP是实施在一个无向图上，而EAX for VRPTW实施在有向图上。

要保证 step 4 生成的临时解有效需要符合两个条件:

每一个customer node都一个indegree和一个outdegree
与depot关联的有m条路线

经过step1,2,3，从 $p_B$ 继承的边的方向，保证了step4中临时解的有效性。

相对的EAX for CVRP 生成的临时解不需要考虑方向(AB-cycle的形成不考虑方向)如下图:

Fig4

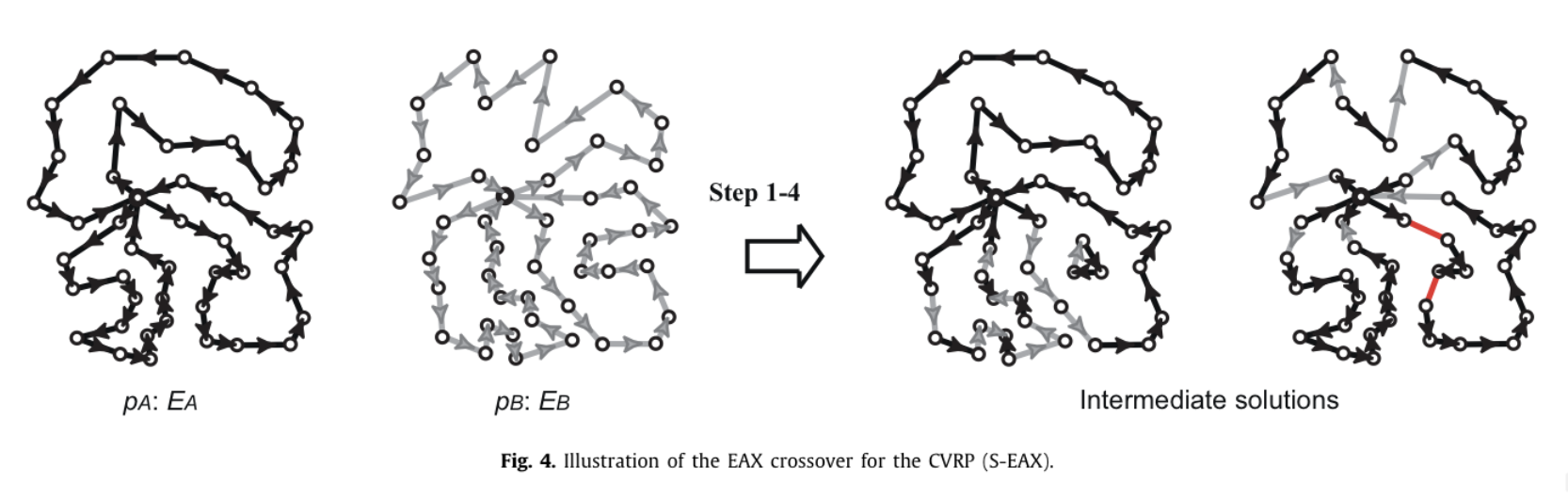
根据是否关心放心，可以把EAX分别称为asymmetric EAX(A-EAX)和symmetric EAX(S-EAX)

虽然S-EAX也可以用于VRPTW（例如通过路线中的边的方向选举），但是A-EAX能尽可能维持了路线中customer中的原有顺序。这将大大减少违反TW约束的情况（对Capacity 约束无帮助）。

3.4 使用的邻域

repair过程和improve过程都是基于传统领域的两种不同的hill-climbing 方法。先定义使用到的领域。

$N(v,\sigma)$：表示与customer v 移动有关的子邻域，有如下 4 种:

$\text{2-opt}^*(v,\sigma)$:
- Remove ($v, v^-$) and ($w, w^+$), and add ($v,w$) and ($v^−, w^+$).
- Remove ($v,v^+$) and$ (w, w^−)$, and add$ (v, w)$ and $(v^+, w^−)$.
$\text{Out-Relocate}(v,\sigma)$: 将 $v$ 插入 $w$ 之前或 $w$ 之后
- Insert $v$ between $w$ and $w^−$, and link $v^−$and $v^+$.
- Insert $v$ between $w$ and $w^+$, and link $v^−$and $v^+$.
In-Relocate$(v,\sigma)$: 将 $w$ 插入 $v$ 之前或 $v$ 之后
- Insert $w$ between $v$ and $v^−$, and link $w^−$and $w^+$.
- Insert $w$ between $v$ and $v^+$, and link $w^−$ and $w^+$.
Exchange$(v,\sigma)$: $v$ 和 $w^-$ 交换或者$v$ 和 $w^+$ 交换
- Insert $v$ between $w$ and $(w^−)^−$, and insert $w^−$between $v^−$and $v^+$.
- Insert $v$ between $w$ and $(w^+)^+$, and insert $w^+$between $v^+$and $v^-$.

w表示在customer v临近的$N_{near}$个customers内的某个customer，$N_{near}$是一个参数，通常设置为50。
$v^-(w^-)$和$v^+(w^+)$分别表示前驱和后继，可以是depot或者customer。
$\text{2-opt}^*$必须是两条不同的路线，其他子邻域可以是相同的路线

3.5 Repair过程

Fig 5

Step 1: 随机选择一条不可行路线 r (违反capactiy或tw).

Step 2: 令 $v \in r$ ，搜索可能的 $N(v,\sigma)$ 得到新的solution $\sigma^\prime$ 使得：

只接收对整个solution的惩罚项有所改进的solution($\alpha\cdot \Delta P_c(\sigma)+\beta\cdot\Delta P_{tw}(\sigma)<0$)
使广义的cost function最小

Step 3: 如果在Step 2 中，路线 r 不存在$v$ 使得 $N(v,\sigma)$ 得到的路线r可行，意味着不可能获得可行解。这个时候放弃repair过程

Step 4: 重复Step1,2直到所有路线都可行。

Repair过程不会采用In-Relocate neighborhood，因为不会对惩罚项有改进。
广义cost function能在O(1)内计算出。$P_c(\sigma)$ computed in O(1)²¹，$P_{t w}(\sigma)$ computed in O(1)见命题1
为了减少迭代次数，和避免大面积的修改继承的边。lines 3, 4采用best-acceptance 策略。
邻域搜索可能会占用大量的计算时间，因此搜索的时候进行一些限制(具体细节见命题2)
- Step 1中优先选择tw不可行的路线。
- 如果选择的是tw不可行路线 r，Step 2 中对路线r 本身的惩罚项没有改进的move将被忽略。判断某个move是否该被忽略计算时间为O(1)。

3.6 Improve 过程

如果repair过程产生可行解，接下来进行 Improve local search。如下：

Fig6

Step 1: 初始化 $V_{n e w}$ ：相对于$p_A$ 发生改变的路线上而引入的新的customer的集合。(即所有的E-set中的customer，以及neiborhood move 所涉及的点)。细节见²⁰

Step 2: 随机选择邻域$N(v,\sigma)$ ,$v \in V_{n e w}$ ，只要$F(\sigma ^\prime) < F(\sigma)$ 则接受（使行驶距离变小）

Step 3: 重复Step1, 2 ，直到没有move 可以改进

3.7 生成初始种群

route minimization(RM) for VRPTW¹⁹（用于决定用车数m和生成初始种群），详细过程如下:

Step 1: 一个customer单独分配一辆车作为初始解。

Step 2: 随机选择一条路线摧毁，路线中的cutomer临时放入ejection poll(EP)中。

Step 3: 不断的将EP中的customer 在不违反capacity和tw 约束的情况下，插回路线中。

Step 4: 如果EP中的某个custoemr不存在可插入位置，那么从现存路线中弹出一些customers，为该customer创建出一个可插入位置。(被弹出的customers加入到EP)

Step 5: 不断重复Step 2-4。直到终结条件满足。

Step 6: 如果是决定用车数m，RM的终结条件为

m 达到lower bound $\lceil \sum _{v=1}^N q_v/Q\rceil$
或者执行时间超过限制$T_1$(通常$T_1$ = 10 min)。
或者持续$T_1^\prime$(<$T_1$)内，EP 的customer数量大于等于$n_u$(通常$n_u$=5)，这种情况下用车数不太可能再减少。

Step 7: 一旦用车数m确定, 其他独立的RM过程（为了生成初始种群）也确定了终结条件为

用车数达到m
执行时间超过$T_1$

为了生成初始种群会不断的运行RM过程，直到$N_{p o p}$个solution产生。如果超过$T_{t o t a l}$时间，如果有效解的数量不足，将进行一些复制。

Step 4.中弹出customer的细节并没有描述，类似于guided local search ²³

4. 计算实验

4.1 实验设置

EAMA参数:

$N_{p o p} = \lceil 20000/N\rceil$, $N_{c h}$ = 20 , $g_{m a x}$ = 50

广义cost function参数:

$\alpha = 1.0$ , $\beta = 1.0$

neighborhood参数:

$N_{n e a r}$ = 50

RM参数:

$T_1 = 10\ min$, $T 1^\prime = {N/10}s$ , $T{total}= NN_{pop}/400 \ min$ , $n_u = 5$

由于这篇论文描述的算法整体效率不高，所以详细的计算结果没有太大的参考意义。故省略

4.4 惩罚项系数的敏感性分析

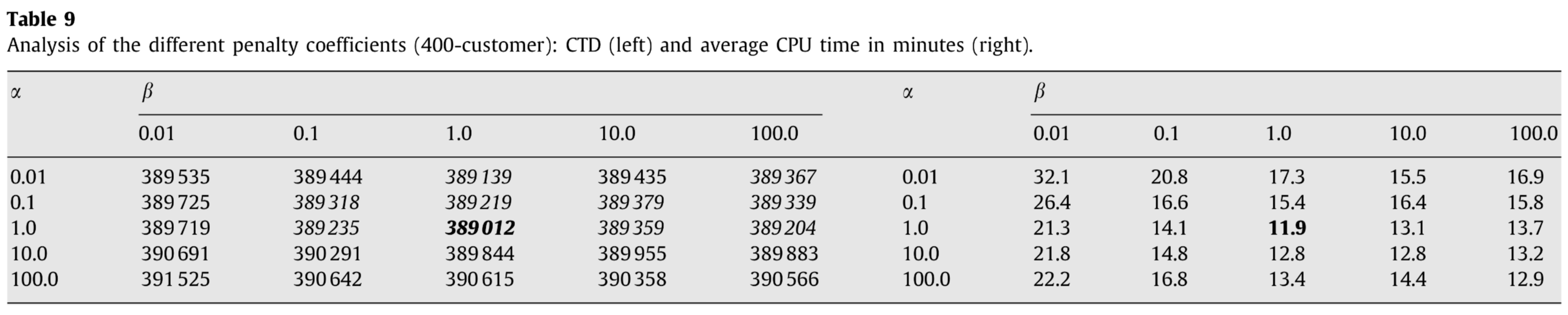
Table 9 分别对计算效果和计算时间的影响。

$\alpha$ 和$\beta$ 的取值对计算效果的影响在0.1%内。
对计算时间的影响较大，主要表现在repair过程和local search 过程的trade-off。如果提升惩罚项系数能减少repair过程的迭代数，生成的临时可行解的质量降低，再后续的Improve过程迭代数反而会上升。

5. 结论

略

6. 附录

$P_{tw}(\sigma)$计算

3.2 中等式$\eqref{4},\eqref{5}$ 定义了给定路线$\langle v_0,v_1,…,v_n,v_{n+1}\rangle$的tw惩罚项$TW(r)$。

我们定义一下node $v_i$ 的forward tw penalty slack，记为$TW_{v_i}^\to$，表示路线上从$v_0$(depot)到$v_i$ 必须补偿的tw惩罚。注意在补偿惩罚后,$v_i$的depart time 可以定义为${\tilde a_{v_i}}$ : $$ TW_{v_i}^\to=\sum_{j=0}^i\max\lbrace \tilde a_{v_j}^\prime - l_{v_j},0\rbrace,\ \ \ \ \ (i=0,…,n+1)\tag{6} $$ 相似的，定义node $v_i$ 的backwark tw penalty slack，记为$TW_{v_i}^\leftarrow$，表示路线上从$v_i$到$v_{n+1}$必须补偿的tw惩罚。先递归的定义一个extened depart time $\tilde z_{v_i}$: $$ \begin{array} \tilde z_{v_i}^\prime = \begin{cases} \ l_0, &i=n+1\\\
\tilde z_{v_{i+1}} - c_{v_{i} v_{i+1}} -s_{v_i} & i=n,\ldots,0 \end{cases}\\\
\tilde z_{v_i} = \begin{cases} \min\lbrace \tilde z_{v_i}^\prime,l_{v_i}\rbrace, &if\ \tilde z_{v_i}^\prime\ge e_{v_i} \\\
\tilde e_{v_i} &if\ \tilde z_{v_i}^\prime\lt e_{v_i} \end{cases} \end{array}\tag{7} $$

$$ TW_{v_i}^\leftarrow = \sum_{j=i}^{n+1}\max\lbrace e_{v_j}-\tilde z\prime_{v_j},0\rbrace,\ \ \ \ \ \ (i=0,…,n+1)\tag{8} $$

如下图Fig7. 圆点分别表示forward和backward方式下计算的depart time $\tilde a_v$和$\tilde z_v$ Fig7

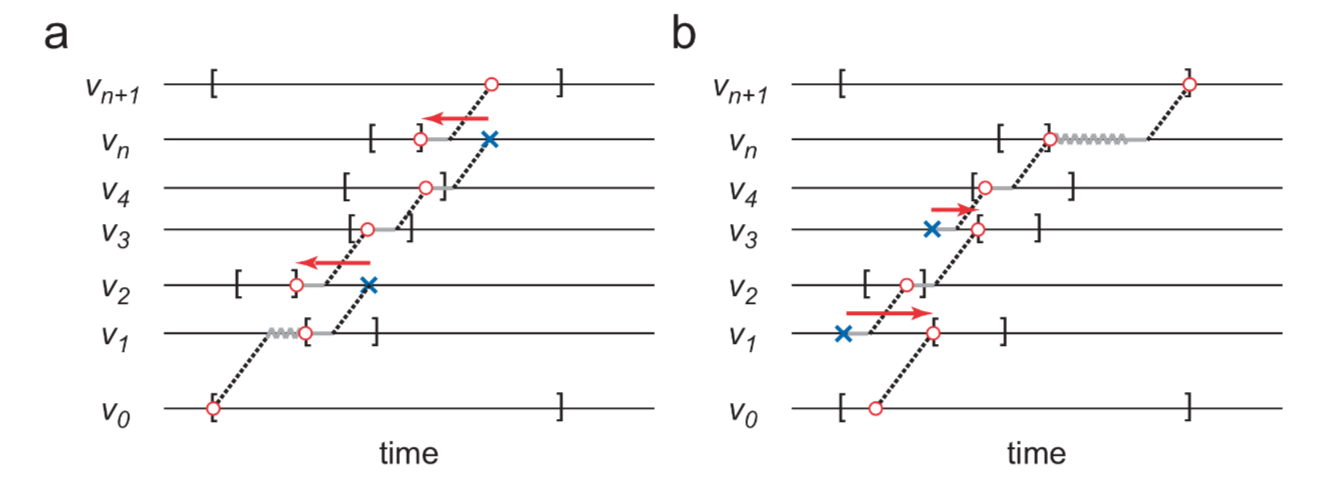
如果$\tilde a_{v_i} \le \tilde z_{v_i}$，没有额外的惩罚引入，否则需要加上惩罚$(\tilde a_{v_i}-\tilde z_{v_i})$，意味着在$v_i$点,depart time可以从$\tilde a_{v_i}$前移至$ \tilde z_{v_i}$

$\tilde z_{v_i}$ 的定义表示，路线的可行性以及tw惩罚或者说tw slack，可以从后往前构建。

我们可以得到下面三个等式： $$ TW(r)=TW_{v_i}^\to + TW_{v_i}^\leftarrow+\max\lbrace\tilde a_{v_i}-\tilde z_{v_i},0\rbrace\tag{9a} $$

$$ TW(r)=TW_{v_{i-1}}^\to + TW_{v_i}^\leftarrow+\max\lbrace\tilde a_{v_i}^\prime-\tilde z_{v_i},0\rbrace\tag{9b} $$

$$ TW(r)=TW_{v_{i-1}}^\to + TW_{v_{i-1}}^\leftarrow+\max\lbrace\tilde a_{v_i}^\prime-\tilde z_{v_i}^\prime,0\rbrace\tag{9c} $$

对于整个solution，我们可以维护4个全局的属性$\tilde a_v^\prime$,$\tilde z^\prime_v$,$TW^\to_v$,$TW_v^\leftarrow$，由此neiborhood move 可以在O(1)内计算。也可以引申出两个结论：

命题1(证明略):

已知两段path:$\langle0,…,x\rangle$,$\langle0,…,y\rangle$，路线$\langle0,…,x,y,…,0\rangle$的惩罚项可以在常数时间内计算。

已知两段path:$\langle0,…,x\rangle$,$\langle0,…,y\rangle$，路线$\langle0,…,x,v,y,…,0\rangle$的惩罚项可以在常数时间内计算。

命题2(证明略):

给定一条路线$\langle0,…,v^-,v,v^+,…,0\rangle$，如果$TW_{v^-}^\to + TW_{v^+}^\leftarrow=TW(r)$，那么除了路线内部交换的任何$N(v,\sigma)$ 都不会使这条路线的惩罚项下降。

Chabrier A. Vehicle routing problem with elementary shortest path based column generation. Computers & Operations Research 2006;33(10):2972–90 ↩︎
Irnich S, Villeneuve D. The shortest path problem with resource constraints and k-cycle elimination. INFORMS Journal on Computing 2006;18(3):391–406. ↩︎
Jepsen M, Spoorendonk S, Petersen B, Pisinger D. A non-robust branch-and- cut-and-price algorithm for the vehicle routing problem with time windows.Jepsen M, Spoorendonk S, Petersen B, Pisinger D. Subset-row inequalities applied to the vehicle-routing problem with time windows. INFORMS Journal on Operations Research 2008;56(2):479–511 ↩︎
Kallehaugea B, Larsenb J, Madsena OBG. Lagrangian duality applied to the vehicle routing problem with time windows. Computers & Operations Research 2006;33(5):1464–87. ↩︎
Mester D, Br¨ aysy O. Active guided evolution strategies for large scale vehicle routing problems with time windows. Computers & Operations Research 2005;32(6):1593–614 ↩︎
Homberger J, Gehring H. Two-phase hybrid metaheuristic for the vehicle routing problem with time windows. European Journal of Operational Research 2005;162:220–38. ↩︎
Bent R, Hentenryck P. A two-stage hybrid local search for the vehicle routing problem with time windows. Transportation Science 2004;38(4):515–30 ↩︎
Pisinger D, Ropke S. A general heuristic for vehicle routing problems. Computers & Operations Research 2007;34(8):2403–35 ↩︎
Prescott-Gagnon E, Desaulniers G, Rousseau L-M. A branch-and-price-based large neighborhood search algorithm for the vehicle routing problem with time windows. Working paper, University of Montreal, Canada; 2007 ↩︎
Ibaraki T, Kubo M, Masuda T, Uno T, Yagiura M. Effective local search algorithms for the vehicle routing problem with general time window constraints. ↩︎
Ibaraki T, Imahori S, Nonobe K, Sobue K, Uno T, Yagiura M. An iterated local search algorithm for the vehicle routing problem with convex time penalty functions. Discrete Applied Mathematics 2008; 156(11):2050–69. ↩︎
Lim A, Zhang X. A two-stage heuristic with ejection pools and generalized ejection chains for the vehicle routing problem with time windows. INFORMS Journal on Computing 2007;19(3):443–57 ↩︎
Homberger J, Gehring H. Two evolutionary meta-heuristics for the vehicle routing problem with time windows. INFORMS Journal on Computing 1999;37(3):297–318 ↩︎
Moscato P. On evolution, search, optimization, genetic algorithms and martial arts towards memetic algorithms. C3P Report 826, California Institute of Technology; 1989. ↩︎
Nagata Y, Kobayashi S. Edge assembly crossover: a high-power genetic algorithm for the traveling salesman problem. In: Proceedings of the 7th international conference on genetic algorithms, 1997. p. 450–7. ↩︎
Nagata Y. Fast EAX algorithm considering population diversity for traveling salesman problems. In: Proceedings of the 6th international conference on EvoCOP2006, 2006. p. 171–82 ↩︎
Nagata Y. New EAX crossover for large TSP instances. In: Proceedings of the 9th international conference on parallel problem solving from nature, 2006. ↩︎
Nagata Y. Edge assembly crossover for the capacitated vehicle routing problem. ↩︎
Nagata Y, Br¨ aysy O. A powerful route minimization heuristic for the vehicle routing problem with time windows, Operations Research Letters, in press. ↩︎
Nagata Y, Br¨ aysy O. Efficient local search limitation strategies for vehicle routing problems. In: Proceedings of the 8th European conference on evolutionary computation in combinatorial optimization, 2008. p. 48–60 ↩︎
Kindervater G, Savelsbergh M. Vehicle routing: handling edge exchanges. In: Aarts E, Lenstra JK, editors. Local search in combinatorial optimization. New York: Wiley; 1997. p. 337–60. ↩︎
Potvin J-Y, Rousseau J-M. An exchange heuristic for routing problems with time windows. Journal of the Operational Research Society 1995;46:1433–46. ↩︎
Voudouris C, Tsang E. Guided local search. In: Glover F, editor. Handbook of metaheuristics. Dordrecht: Kluwer; 2003. p. 185–218. ↩︎

Contents